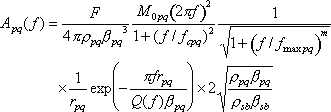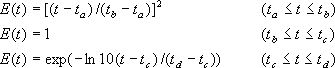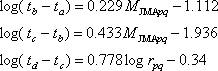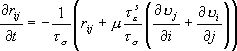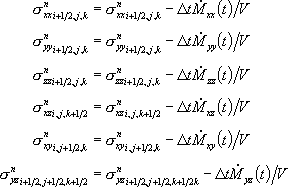6.詳細法による地震動時刻歴および地震動予測地図
6.1 計算手法
6.1.1で計算の手順を述べ、6.1.2では計算手法の詳細に関して述べる。図6.1-1に計算手順を示す。本章では地盤の深度レベルに応じて計算手法やモデルを説明するため、図6.1-1のように地盤に関する用語を定義する。
6.1.1 計算手順
(1)手順[1]:深部地盤上面における波形計算
- 深部地盤上面における波形をハイブリッド合成法により求める。ハイブリッド合成法は、長周期成分を理論的方法(Pitarka (1999) による不等間隔格子有限差分法)、短周期成分を統計的グリーン関数法(壇・他 (2000) )によりそれぞれ計算し、合成する方法である。
(2)手順[2]:詳細法工学的基盤における波形計算
- 図6.1-1に示すように、深部地盤の上面のS波速度(
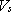 )は800m/sであり、さらに、この深部地盤の上面以浅に )は800m/sであり、さらに、この深部地盤の上面以浅に 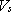 =500m/sに至る速度層を設定している地域がある。そのような地域では、深部地盤上面の波形を入力波形とし、1次元重複反射理論により周波数増幅関数を評価して =500m/sに至る速度層を設定している地域がある。そのような地域では、深部地盤上面の波形を入力波形とし、1次元重複反射理論により周波数増幅関数を評価して 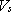 =500m/s層の上面における波形を求めた。本報告では、 =500m/s層の上面における波形を求めた。本報告では、 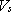 =500m/sに至る層があるところではその上面、そのほかのところでは深部地盤の上面を連続した面とみなし、詳細法工学的基盤と定義した。したがって、詳細法工学的基盤での波形といえば、 =500m/sに至る層があるところではその上面、そのほかのところでは深部地盤の上面を連続した面とみなし、詳細法工学的基盤と定義した。したがって、詳細法工学的基盤での波形といえば、
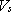 =500m/s層のあるところでは =500m/s層のあるところでは 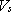 =500m/s層上面の波形を指し, =500m/s層上面の波形を指し, 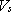 =500m/s層の無いところでは深部地盤上面における波形を指す。詳細法工学的基盤におけるS波速度は、500m/sから800m/sまでの幅を有していることに注意が必要である。 =500m/s層の無いところでは深部地盤上面における波形を指す。詳細法工学的基盤におけるS波速度は、500m/sから800m/sまでの幅を有していることに注意が必要である。
(3)手順[3]:地表における最大速度の計算
- 詳細法工学的基盤から地表までの最大速度増幅率を算定し、これを詳細法工学的基盤での最大速度に乗じて地表における最大速度を求める。詳細法工学的基盤から地表までの最大速度増幅率は、3章「地下構造モデルの設定」で示された工学的基盤(S波速度400m/s相当)から地表までの増幅度に、詳細法工学的基盤から工学的基盤までの増幅度の補正係数を乗じて求める。増幅度の補正係数は、松岡・翠川 (1994) による表層地盤の速度増幅度算定式 (6.1-1) 式にそれぞれのS波速度を代入して算定された速度増幅度の比とする。すなわち補正係数は(詳細法工学的基盤のS波速度/400)0.66で算定される。ただし、詳細法工学的基盤のうち (6.1-1) 式の適用範囲である
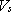 =1500m/sを超えるところについては、ここでは =1500m/sを超えるところについては、ここでは 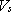 =1500 m/sとして処理することにより、増幅度を頭打ちさせた。 =1500 m/sとして処理することにより、増幅度を頭打ちさせた。
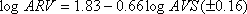 |
(6.1-1) |
( 100 < 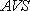 < 1500 ) < 1500 ) |
|
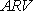 |
: 地下30m から地表までの速度増幅率 |
|
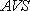 |
: 地下30m から地表までの平均S波速度(m/s) |
|
(4)手順[4]:地表における計測震度
- 計算された地表最大速度より、次の (6.1-2) 式に示す翠川・他 (1999) による最大速度と計測震度の経験的関係式を用いて、計測震度相当値を算定した。
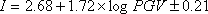 |
( 4 < 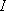 < 7 ) < 7 ) |
(6.1-2) |
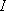 :計測震度 :計測震度 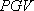 :地表最大速度(cm/s) :地表最大速度(cm/s) |
|
- なお、翠川・他 (1999) では0<
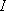 <7の式と4< <7の式と4< 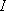 <7の2つの式が提示されているが、0< <7の2つの式が提示されているが、0< 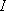 <7の式は低震度データが強く反映され高震度データがあまり反映されない怖れがあり、かつ計測震度と旧気象庁震度との関係のばらつきも高震度になるほど小さくなる傾向があるため、比較的震度の大きな地域での地震動をより精度良く評価することが重要と考え、4< <7の式は低震度データが強く反映され高震度データがあまり反映されない怖れがあり、かつ計測震度と旧気象庁震度との関係のばらつきも高震度になるほど小さくなる傾向があるため、比較的震度の大きな地域での地震動をより精度良く評価することが重要と考え、4<
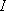 <7の式を選定した。 <7の式を選定した。
以下、ボーリング地点における個別評価を示す。
(5)手順[5]:地表面における波形(最大速度)
- それぞれのボーリング地点において前述の手順[2]により求められた詳細法工学的基盤における波形を入力波形として、等価線形法により地表波形を計算した。等価線形法には、代表的なプログラムであるSHAKE(Shnabel
et al., 1972)を使用した。最大速度は、速度波形より読み取った。
(6)手順[6]:地表面における計測震度
- ボーリング地点では、地表面における水平2成分の地震波形が計算される。地震波形から計測震度を計算するには、3成分(直交水平2成分+鉛直成分)の地震波形が必要である
(斎藤, 1996) が、ここでは鉛直成分の振幅は零であるとして、計測震度を計算することとした。一般的に水平動より上下動の方がその振幅が小さいため、計測震度の値にはほとんど影響しない。
(1)ハイブリッド合成法
ハイブリッド合成法は、短周期領域での地震動を統計的グリーン関数法で、長周期領域を3次元差分法で算定し、最終的に両者を重ね合わせて広帯域地震動を作成する方法である。この手法の特徴は、地盤や断層の不均質性の影響を受けにくく波動モデルで説明可能な長周期地震動を物理モデルに基づいて理論的に計算し、逆に地盤や断層の不均質性の影響を受け易く統計的にしか説明できない、もしくは理論的な計算効率が悪い短周期地震動を統計的に計算することである。両領域を接続する周期は、地下構造データや振動特性、差分法計算に用いる計算機の能力を考慮して決定する。短周期成分はハイパスフィルタ処理を、長周期域成分はローパスフィルタ処理を行った後、両者を重ね合わせて接続する(このフィルタをマッチングフィルタと呼ぶ)。両フィルタとも接続周期
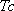 で0.5となるコサイン型(-90°〜90°)で、 で0.5となるコサイン型(-90°〜90°)で、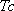 /1.4〜 /1.4〜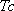 /0.6の周期幅で1から0に減衰する。ここでは、接続周期を1秒とした。 /0.6の周期幅で1から0に減衰する。ここでは、接続周期を1秒とした。
(2)統計的グリーン関数法
(a) 地震基盤における統計的グリーン関数の作成
地震基盤における統計的グリーン関数は、佐藤(1994a、1994b)が仙台地域で観測された主に海溝型地震の記録から推定したパラメータを用いたスペクトルモデルと経時特性モデルを用いて、Boore(1983)と同様の手法で作成した。
地震基盤における S 波主要動のスペクトルは、次式で表わされる地震動の加速度フーリエスペクトルのモデルによって表現した。
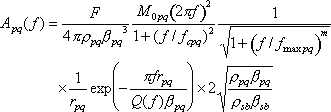
ここに、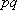 は要素断層に関する添字で、 は要素断層に関する添字で、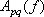 は地震動の加速度フーリエスペクトル、 は地震動の加速度フーリエスペクトル、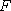 は地震波の放射特性、 は地震波の放射特性、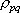 および および 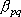 は要素断層における地殻の密度および剪断波速度、 は要素断層における地殻の密度および剪断波速度、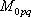 は地震モーメント、 は地震モーメント、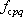 は臨界振動数、 は臨界振動数、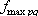 は高周波遮断振動数、 は高周波遮断振動数、 は定数、 は定数、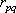 は震源距離、 は震源距離、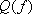 は地殻の は地殻の 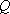 値、 値、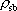 および および 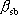 は地震基盤の密度および剪断波速度である。 は地震基盤の密度および剪断波速度である。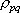 および および 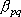 は震源における密度2.7 は震源における密度2.7 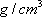 、S波速度3.5 、S波速度3.5 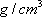 である。最終項は、自由表面の影響および要素断層における地殻のインピーダンスと地震基盤のインピーダンスとの相違 (佐藤, 1978) を考慮した項である(壇・他 (2000))。 である。最終項は、自由表面の影響および要素断層における地殻のインピーダンスと地震基盤のインピーダンスとの相違 (佐藤, 1978) を考慮した項である(壇・他 (2000))。
地殻の 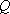 値である 値である 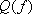 は、 は、
で表される値とした。(6.1-3) は、佐藤・他(1994b)の推定値であるが、最近の研究では、0.8Hz前後以下で 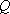 値が頭うちするあるいは減少することが指摘されていることから、 (6.1-4) のように0.8Hz以下で一定値とする。 値が頭うちするあるいは減少することが指摘されていることから、 (6.1-4) のように0.8Hz以下で一定値とする。
要素断層の大きさは、4章で述べたように2km×2kmである。断層モデルの中心点付近で、地震モーメント 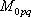 を3.28×1023 dyn-cm、断層の長さ を3.28×1023 dyn-cm、断層の長さ 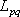 を 2 km 、幅 を 2 km 、幅 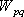 を 2 km 、実効応力 を 2 km 、実効応力 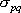 を 10MPaとして、統計的グリーン関数を作成した。なお、 を 10MPaとして、統計的グリーン関数を作成した。なお、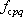 は以下の式から算出できる。 は以下の式から算出できる。
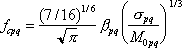
さらに、強震動を評価する領域内にある 1地点を考えると、その地点は各要素断層から見て常に同じ方位に位置しているわけではないこと、および、短周期の地震記録には明確な放射特性が見られないことから、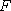 は平均的な値を用いることとした。計算地点と断層面との幾何学的関係および断層の滑りのタイプを考慮して、Boore and Boatwright
(1984) に示された は平均的な値を用いることとした。計算地点と断層面との幾何学的関係および断層の滑りのタイプを考慮して、Boore and Boatwright
(1984) に示された 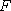 の値のうちSH 波 (S 波のうち重力の方向に直交する成分) とSV 波 (S 波のうち SH 波に直交する成分) の値の大きい方を採用した。 の値のうちSH 波 (S 波のうち重力の方向に直交する成分) とSV 波 (S 波のうち SH 波に直交する成分) の値の大きい方を採用した。
一方、時刻歴波形の作成には経時特性あるいは位相特性が必要であるが、地震基盤におけるS波主要動の経時特性に関しては現在までに十分な研究成果が得られていない。
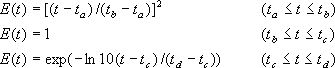
ここに、
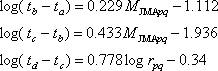
である。気象庁マグニチュードは、佐藤(1995) に基づいて、地震モーメント 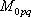 から算出した。 から算出した。
(b) 深部地盤上面での統計的グリーン関数の作成
各計算ポイント直下の三次元地盤モデルから、計算ポイント毎に1次元地盤モデルを作成し、(a)において作成された地震基盤における統計的グリーン関数を入射波とし、S波の1次元重複反射理論により、3次元地盤構造モデル上面での統計的グリーン関数を計算する。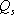 値は、(6.1-3)、(6.1-4)と同じである。これは、佐藤・他(1994b)において、仙台で観測された強震記録のスペクトルインバージョンに基づき求められた経験的地盤増幅率が 値は、(6.1-3)、(6.1-4)と同じである。これは、佐藤・他(1994b)において、仙台で観測された強震記録のスペクトルインバージョンに基づき求められた経験的地盤増幅率が 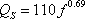 を用いた1次元地盤モデルによりほぼ説明できることが示されているためである。 を用いた1次元地盤モデルによりほぼ説明できることが示されているためである。
(c) 深部地盤上面における統計的グリーン関数を用いた波形合成
(b) で作成された深部地盤上面における統計的グリーン関数を用いて、壇・佐藤(1998)の断層の非一様滑り破壊を考慮した半経験的波形合成法により波形合成を行なう。この際,大地震の要素断層の滑り量と応力降下量が再現されるように、震源スペクトルを補正した。このようにして算定された要素断層の波形を大地震の断層面全体の破壊過程を考慮して合成した。
(3)3次元差分法
(a) 計算範囲(吸収境界を除く)
- 南西端:東経139.6725 北緯37.8321
- 南東端:東経140.6723 北緯37.8377
- 北西端:東経139.6521 北緯39.0933
- 北東端:東経140.6695 北緯39.0991
- 東西 :88km
- 南北 :140km
(b) 計算仕様
- 最小セルサイズ:100m
- 総格子数(吸収境界を含む):130×921×1441=172,530,930
- 時間ステップ:62.5msec
- 計算時間:102.4秒(16,384ステップ)
- 応力−速度スタガードグリッド(図6.1-2、Levander (1988))
- 不等間隔格子(Pitarka,1999)
- メモリー変数を用いた粘弾性計算(Robertsson, 1994)
(c) 近似度数
(d) 基本式
- 三次元 (
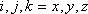 ) の波動場計算は下記の式を差分化して行った。使用するリラクゼーションメカニズムの数はひとつである。応力テンソルの対角成分は下記の式で計算する( ) の波動場計算は下記の式を差分化して行った。使用するリラクゼーションメカニズムの数はひとつである。応力テンソルの対角成分は下記の式で計算する(
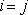 )。 )。
-
- 応力テンソルの非対角成分は下記の式で計算する(
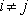 )。 )。
-
- メモリー・バリアブルの対角成分は下記の式で計算する。
-
- メモリー・バリアブルの非対角成分は下記の式で計算する。
-
- 粒子速度はニュートンの法則より下記の式で計算する。
-
- ここで、
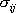 は は 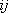 成分の応力テンソル、 成分の応力テンソル、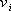 は は 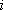 成分の粒子速度、 成分の粒子速度、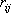 は は 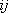 成分のメモリー・バリアブル、 成分のメモリー・バリアブル、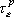 、 、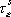 は、それぞれPおよびS波に対する歪みリラクゼーション・タイム、 は、それぞれPおよびS波に対する歪みリラクゼーション・タイム、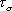 は応力リラクゼーション・タイム、 は応力リラクゼーション・タイム、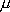 はS波に対するレラクゼーション・モジュラス(MR)、 はS波に対するレラクゼーション・モジュラス(MR)、 はP波に対するリラクゼーション・モジュラス(MR)、 はP波に対するリラクゼーション・モジュラス(MR)、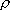 は密度である。 は密度である。
(e) 地表の境界条件
- 自由表面(Z=0)では、表面に直行する下記の応力テンソルおよび対応するメモリーバリアブルをゼロとする。
-
(f) 吸収境界条件
- Cerjan (1985) を用いた。吸収境界の厚さは20格子(2km)とした。
(g) 不等間隔格子
- 図6.1-3に示すように深度方向に格子サイズを変更する。
- 四次近似の場合の係数は下記の式で計算される(図6.1-4)。
-
- ただし、
-
- である。深度方向の格子サイズは表6.1-1のとおりである。水平方向の格子サイズは100mである。
(h) 粘弾性計算
- 周期に対する
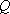 の近似は図6.1-5のとおりである( の近似は図6.1-5のとおりである(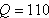 の場合)。 の場合)。
(i) 震源
- Pitarka (1999) に基づき、下記のように応力テンソルにモーメントテンソルの時間微分を加算する。
-
- ここで、
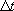 は時間ステップ、 は時間ステップ、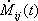 はモーメントテンソルの時間微分、 はモーメントテンソルの時間微分、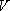 は震源となる格子の有効体積である。小震源は断層面に沿って400m間隔で格子上に設けた。 は震源となる格子の有効体積である。小震源は断層面に沿って400m間隔で格子上に設けた。
(j) すべり速度時間関数
- 中村・宮武 (2000) の近似式を用いた。図6.1-6にすべり速度時間関数のスペクトルを示した。同図にはベル型(1秒、2秒)のスペクトルも示している。
|