6.2 計算結果
詳細法により深部地盤上面における地震動の時刻歴を求め、また、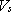 =500m/s層が分布する地域ではさらにその層の増幅を考慮した上で、地震動の時刻歴の最大速度に地盤増幅率をかけて地表の速度を求める。次に、地表の速度から換算式によって計測震度を求める。 =500m/s層が分布する地域ではさらにその層の増幅を考慮した上で、地震動の時刻歴の最大速度に地盤増幅率をかけて地表の速度を求める。次に、地表の速度から換算式によって計測震度を求める。
ここでは、統計的グリーン関数法、3次元有限差分法、ハイブリッド法のそれぞれの結果についてまとめる。計算ケースは表6.2-1に示すとおりである。
6.2.1 統計的グリーン関数法による強震動予測
図6.2-1に深部地盤上面から地表までの増幅倍率を示す。
図6.2-2に統計的グリーン関数法による深部地盤上面における最大速度分布を示す。図6.2-3に地表における最大速度分布を示す。図6.2-4に震度分布を示す。図6.2-5に司・翠川 (1999)式の距離減衰式と統計的グリーン関数法による計算結果との比較を示す。
6.2.2 3次元有限差分法による地震動予測結果
予測結果として、以下の内容についてまとめる。
- (1)測線沿いの地表波形
- (2)K-NETおよびKiK-net地点の波形一覧図
- (3)各地点の波形とスペクトル
(1)測線沿いの深部地盤構造モデル上面の波形
ケース2およびケース3について、東西測線沿いに深部地盤上面の波形を表示したものを作成した。
図6.2-6は、深部構造モデルの深度400m〜500mの速度構造に、深部地盤上面の波形を表示する東西測線の位置を示している。X=20kmは米沢盆地、X=50〜80kmは山形〜村山、X=100km鶴岡〜新庄のあたりとなっている。
図6.2-7(1)〜(6) はケース2の東西測線の深部地盤構造モデル上面の波形を示しており、図6.2-8(1)〜(6) はケース3の波形を示している。これらの図は、最上段に速度構造モデルの東西方向の深度スライスで東西が92km、深度方向が57kmで、縦横のスケールは1:1となっている。この断面に沿った深部地盤上面の波形(3成分)を、その下に表示した。上から南北(黒)、東西(青)、上下(緑)である。それぞれの成分の波形は、上側が西側で、西から東に並んでいる。波形は1kmおきの波形である。振幅は各図の最大振幅でノーマライズしているので、1枚の図の中では相対振幅は保存しているが、異なる図同士の振幅は比較できない。
これらの図によると、震源断層より東側で振幅が大きくなっていること、地震基盤が深い盆地で継続時間が長くなっていることなどが見られる。
(2)K-NETおよびKiK-net地点の波形一覧図
計算領域内のK-NETおよびKiK-net地点について、深部地盤上面( 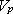 =2.2km/s、 =2.2km/s、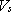 =0.8km/s)におけるNS成分、EW成分、UD成分の3成分の速度波形を地図上に図化したものを図6.2-9〜図6.2-12に示した。 =0.8km/s)におけるNS成分、EW成分、UD成分の3成分の速度波形を地図上に図化したものを図6.2-9〜図6.2-12に示した。
どのケースも断層の東側で波形の振幅が大きくなっている。特に、破壊の進行方向で大きくなっている。また、破壊開始側のアスペリティ近傍では、EW成分の振幅が大変大きくなっている。
(3)各地点の波形とスペクトル
震源のすべり速度時間関数の違いによる波形とスペクトルの比較を行った。
比較を行ったのは、以下の4地点である。
ここで対象とした波形は速度波形、スペクトルは変位の振幅スペクトルである。
4地点ごとに、ベル型(1秒)による波形、ベル型(1秒)の1Hzハイカットの波形、中村・宮武による波形、中村・宮武の1Hzハイカットの波形を3成分(UD,NS,EW)ごとに波形を並べて示した。スペクトルは、ベル型1秒と中村・宮武を分けて3成分の波形を重ね書きしている。
速度波形は、最大値はベル型1秒に比べると中村・宮武の方が1/4〜1/2程度の大きさとなっている。
スペクトルは、中村・宮武では0.1Hz付近をピークとし、周波数が増すにつれ振幅が小さくなるが、ベル型1秒に比べると落ち方は緩やかである。
6.2.3 ハイブリッド法による強震動予測
図6.2-21にハイブリッド法による深部地盤上面におけるNS成分の最大速度分布を示し、図6.2-22にEW成分の最大速度分布を示す。それぞれ4ケースを1枚の図にまとめている。図6.2-23には、NS成分とEW成分の波形からベクトル合成したものの最大速度分布を示す。
図6.2-24 には、一部の地域に分布する 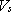 =500m/s 層を考慮した詳細法工学的基盤上面の最大速度分布を示す(深部地盤上面のNS, EW成分の波形から個別に詳細法工学的基盤上面における波形を求め、さらにベクトル合成した)。 =500m/s 層を考慮した詳細法工学的基盤上面の最大速度分布を示す(深部地盤上面のNS, EW成分の波形から個別に詳細法工学的基盤上面における波形を求め、さらにベクトル合成した)。
図6.2-26 には図6.2-24 の詳細法工学的基盤上面の最大速度に微地形区分による増幅倍率(図6.2-25)をかけ、地表の最大速度を求めたものを示す。さらに、図6.2-27 には、翠川・他 (1999)による計測震度と最大速度の関係を用いて、地表での最大速度から計測震度を求めたものを示す。
図6.2-28〜31 には、図2-2 に示した5地点(酒田、新庄、寒河江、米沢、山形)の時刻歴波形を示す。4ケースの震源モデルごとで5地点ごとに加速度波形のNS、EW成分、速度波形のNS,EW成分を1枚にまとめている。
図6.2-32には司・翠川 (1999) の距離減衰式と松岡・翠川 (1994) の微地形区分による増幅倍率を用いた簡易法による最大速度とハイブリッド法による計算結果を比較したものを示す。
|