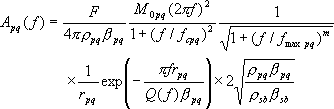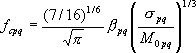4.2.2. 統計的グリーン関数法
A. 地震基盤における統計的グリーン関数の作成
地震基盤における統計的グリーン関数は、佐藤(1994a, 1994b)が仙台地域で観測された主に海溝型地震の記録から推定したパラメータを用いたスペクトルモデルと経時特性モデルを用いて、Boore(1983)と同様の手法で作成した。
地震基盤におけるS 波主要動のスペクトルは、次式で表される地震動の加速度フーリエスペクトルのモデルによって表現した。
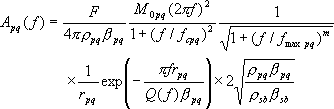 |
(4.2-3) |
ここに、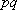 は要素断層に関する添字で、 は要素断層に関する添字で、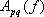 は地震動の加速度フーリエスペクトル、 は地震動の加速度フーリエスペクトル、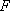 は地震波の放射特性、 は地震波の放射特性、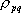 および および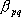 は要素断層における地殻の密度および剪断波速度、 は要素断層における地殻の密度および剪断波速度、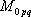 は地震モーメント、 は地震モーメント、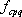 は臨界振動数、 は臨界振動数、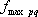 は高周波遮断振動数、 は高周波遮断振動数、 は定数、 は定数、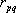 は震源距離、 は震源距離、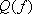 は地殻の は地殻の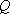 値、 値、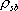 および および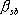 は地震基盤の密度および剪断波速度である。 は地震基盤の密度および剪断波速度である。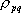 および および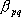 は震源における密度3.03 は震源における密度3.03 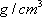 、S 波速度3.93 、S 波速度3.93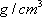 である。最終項は、自由表面の影響および要素断層における地殻のインピーダンスと地震基盤のインピーダンスとの相違(佐藤、1978)
を考慮した項である。 である。最終項は、自由表面の影響および要素断層における地殻のインピーダンスと地震基盤のインピーダンスとの相違(佐藤、1978)
を考慮した項である。
地殻の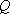 値である 値である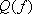 は、 は、
で表される値とした。(4.2−4)式は、佐藤・他(1994b)の推定値であるが、最近の研究では、1Hz
前後以下で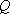 値が頭うちするあるいは減少することが指摘されていることから、1Hz 以下で一定値としている。要素断層の大きさは、4km×4km
である。断層モデルの中心点付近で、地震モーメント 値が頭うちするあるいは減少することが指摘されていることから、1Hz 以下で一定値としている。要素断層の大きさは、4km×4km
である。断層モデルの中心点付近で、地震モーメント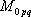 を を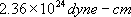 、断層の長さ 、断層の長さ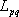 を4km 、幅 を4km 、幅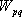 を4km 、実効応力 を4km 、実効応力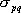 を90bar として、統計的グリーン関数を作成した。なお、 を90bar として、統計的グリーン関数を作成した。なお、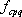 は、以下の式から算出できる。 は、以下の式から算出できる。
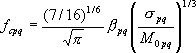 |
(4.2-6) |
さらに、強震動を評価する領域内で、ある1つの地点を考えると、その地点は各要素断層からみて常に同じ方位に位置しているわけではないこと、および短周期の地震記録には明確な放射特性が見られないことから、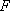 は平均的な値を用いることとした。計算地点と断層面との幾何学的関係、および断層のすべりのタイプを考慮して、Boore
and Boatwright (1984)に示された は平均的な値を用いることとした。計算地点と断層面との幾何学的関係、および断層のすべりのタイプを考慮して、Boore
and Boatwright (1984)に示された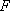 の値のうち、 の値のうち、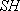 波(S波のうち重力の方向に直交する成分) と 波(S波のうち重力の方向に直交する成分) と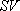 波(S波のうち 波(S波のうち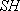 波に直交する成分)の値の大きいほうを採用した。具体的には、dip angle 30°
のdip-slip の 波に直交する成分)の値の大きいほうを採用した。具体的には、dip angle 30°
のdip-slip の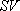 波の値0.62 を採用した。 波の値0.62 を採用した。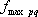 と と は、佐藤・他(1994b)の推定値 は、佐藤・他(1994b)の推定値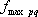 = 13.5 Hz、 = 13.5 Hz、 = 4.2 である。 = 4.2 である。
一方、時刻歴波形の作成には経時特性あるいは位相特性が必要であるが、地震基盤におけるS波主要動の経時特性に関しては、現在までに研究成果が得られていない。しかし、本検討では、最終的に統計的グリーン関数を定義する位置を「詳細法工学的基盤」上とするため、佐藤・他(1994a)の仙台地域の工学的基盤における地震記録から求められた経験的経時特性モデルを準用した。
ここに、
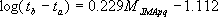 |
(4.2-10) |
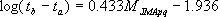 |
(4.2-11) |
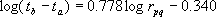 |
(4.2-12) |
気象庁マグニチュード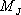 は、佐藤(1989)による次式に基づき、地震モーメント は、佐藤(1989)による次式に基づき、地震モーメント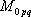 から次式に基づき算出した。 から次式に基づき算出した。
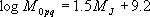 [N・m] [N・m] |
(4.2-13) |
B. 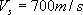 層上面での統計的グリーン関数の作成 層上面での統計的グリーン関数の作成
各計算ポイント直下の三次元地盤モデルから、各計算ポイントでの1次元地盤モデルを作成し、S波の1次元重複反射理論により、A.において作成された地震基盤における統計的グリーン関数を入射波とした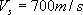 層上面での統計的グリーン関数を計算する。表4.2−2〜表4.2−6 に、波形を示す5 つの地点(図2−3 参照)での地震基盤から「詳細法工学的基盤」までの1次元地盤モデルを示す。なお、 層上面での統計的グリーン関数を計算する。表4.2−2〜表4.2−6 に、波形を示す5 つの地点(図2−3 参照)での地震基盤から「詳細法工学的基盤」までの1次元地盤モデルを示す。なお、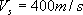 層での増幅については、後述するハイブリッド合成波の段階で考慮する。 層での増幅については、後述するハイブリッド合成波の段階で考慮する。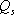 値は、(4.2−4)式、(4.2−5)式と同じとした。これは、佐藤ほか(1994b)において、仙台で観測された強震記録のスペクトルインバージョンに基づき求められた経験的地盤増幅率が 値は、(4.2−4)式、(4.2−5)式と同じとした。これは、佐藤ほか(1994b)において、仙台で観測された強震記録のスペクトルインバージョンに基づき求められた経験的地盤増幅率が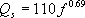 を用いた1 次元地盤モデルによりほぼ説明できることが示されているためである。 を用いた1 次元地盤モデルによりほぼ説明できることが示されているためである。
C. 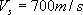 層上面における統計的グリーン関数を用いた波形合成 層上面における統計的グリーン関数を用いた波形合成
B.で作成された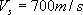 層上面における統計的グリーン関数を用いて、壇・佐藤(1998)の断層の非一様すべり破壊を考慮した半経験的波形合成法に従い、波形合成を行う。この際、大地震の要素断層のすべり量と応力降下量が再現されるように、震源スペクトルの補正を行った。このようにして算定された大地震の要素断層の波形を断層面全体の破壊過程を考慮して合成を行った。 層上面における統計的グリーン関数を用いて、壇・佐藤(1998)の断層の非一様すべり破壊を考慮した半経験的波形合成法に従い、波形合成を行う。この際、大地震の要素断層のすべり量と応力降下量が再現されるように、震源スペクトルの補正を行った。このようにして算定された大地震の要素断層の波形を断層面全体の破壊過程を考慮して合成を行った。
|