4.2. 詳細法
4.2.1. 三次元有限差分法
A. 手法の概要
有限差分法は有限要素法とならんで解析領域全体を離散化して解く方法(領域法)の代表的なものである。具体的には、対象領域内に配置された離散化された節点(格子点)において、波動場を記述する波動方程式の変数にテイラー展開を適用し微係数を差分近似することで格子点での値に関する連立一次方程式(差分方程式)を作成し、これを逐次解いていく方法である。
格子点毎に独立に物理定数が付与できるので不均質性が強い場の問題を解くのに適するほか、非線形の問題にも適用でき、応用範囲が広い。解き得る問題の規模は計算機の記憶容量と計算時間に依存するが、差分法の計算アルゴリズム自体がベクトル化に適しており、他の手法と比べて大規模な数値演算が容易に行える利点がある。また、他の領域型の離散化手法と同様にすべての格子点での応答が同時に得られるので、可視化の技法を使えば地動の面的分布は容易に表現できる。しかし、次に示すような領域法に属する離散化手法が避けて通れない難点がある。第一は、空間上の離散化された格子点すべてに地盤の弾性定数を与えなければならず扱うデータ量が膨大となることである。第二は空間上の離散化によって生じる数値誤差のため計算精度に留意する必要があり、適用できる周波数帯域は格子点間隔から決まる特定の周波数よりも低周波数側に限定されることである。第三は地盤の半無限性(無限境界)の扱いが完全ではないことである。これらに加え、次のような差分法特有の問題点があげられる。差分格子は一般的には等間隔の直交格子が基本となるため、格子点の配置に有限要素法のような融通性がなく複雑な境界条件の扱いも容易ではない。例えば、凹凸がある地表面の応力解放条件を満足させるのは容易ではない。時空間上の有限差分法では計算効率が陰解法と比べて格段に優れている陽解法を採用するのが普通である。陽解法とは各時間ステップ毎の各格子点における解をその点自身とその極く近傍の格子点の数ステップ前までの解を用いて、式を解かずに直接計算するだけで求める方法であり、陰解法に比べて計算に必要な記憶容量が非常に少なくて済み、計算時間も大幅に短縮されるという利点がある。しかし、陽解法を採用する場合、空間および時間の離散化において数値安定性を考慮する必要があり、空間的に変化する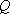 値を導入する場合、近似的な扱いとならざるを得ない。上述したようないくつかの難点もあるが、有限要素法と比べて簡便で計算時間が速いので、最近では大規模な領域を対象とした地震波の波動伝播問題によく用いられている。 値を導入する場合、近似的な扱いとならざるを得ない。上述したようないくつかの難点もあるが、有限要素法と比べて簡便で計算時間が速いので、最近では大規模な領域を対象とした地震波の波動伝播問題によく用いられている。
B. 地盤および波動伝播特性のモデル化と精度
(1) 格子点の配置
媒質の離散化における格子点(グリッド)の配置方法として、食い違い格子あるいはスタッガードグリッド(staggered
grid)と呼ばれるものを用いる。これは、変位(あるいは速度)を評価する格子点と応力を評価する格子点を格子点間隔
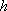 の半分だけずらす方法である(例えば、Virieux and Madariaga, 1982)。変位勾配から歪み・応力が決まるという物理的な性質をよく表しており自然であり、数値安定性が向上する利点がある。ただし、変位(あるいは速度)の各成分の格子点が互いに異なる点にあるため、厳密には同一点での値を求めることができない不自由さがある。図4.2−1 にGraves(1996)の論文に記載されている食い違い格子の模式図を示す。図中、速度の各成分は黒印の点で計算され、応力の各成分は、その黒印の点から半グリッド( の半分だけずらす方法である(例えば、Virieux and Madariaga, 1982)。変位勾配から歪み・応力が決まるという物理的な性質をよく表しており自然であり、数値安定性が向上する利点がある。ただし、変位(あるいは速度)の各成分の格子点が互いに異なる点にあるため、厳密には同一点での値を求めることができない不自由さがある。図4.2−1 にGraves(1996)の論文に記載されている食い違い格子の模式図を示す。図中、速度の各成分は黒印の点で計算され、応力の各成分は、その黒印の点から半グリッド( 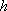 /2)だけずれた白印の点で計算される。また、媒質を規定するパラメータである密度およびラーメの定数(密度、P
波速度、S 波速度を与えればラーメの定数は一意に定まる)は白丸の点毎に独立に与えられる。 /2)だけずれた白印の点で計算される。また、媒質を規定するパラメータである密度およびラーメの定数(密度、P
波速度、S 波速度を与えればラーメの定数は一意に定まる)は白丸の点毎に独立に与えられる。
(2) 離散化誤差と数値安定性
微分演算の差分近似は、微分点の前後での値の変化が十分に小さいことを仮定してテイラー展開を用いて誘導されるので、離散化誤差を小さくするためには格子点間隔を対象波長に対して小さく選ぶ必要がある。格子点間隔を対象波長の何分の一以下にすべきかは差分方程式の近似度(あるいは精度ともいう)によって決まる。微分法の値は近似度4(4
次精度)の場合、その周囲の4つの格子点の値から定まる。三次元波動場の計算に最近よく用いられる差分法は空間に関して近似度4のものが多い(例えば、Frankel
and Vidale, 1992; Graves, 1996;Pitarka, 1999)。実際の計算上の精度を確保するための格子点間隔は、空間に関して近似度4の場合、対象波長の5分の一以下にする必要がある(Levander、1988)。それよりも短い波長の波は減衰させられる(例えば、Buell,
1991; 竹中, 1993)と同時に位相速度の変化(数値分散)が顕著になる。波動方程式を陽解法型の差分方程式に近似して解く場合の差分スキームの安定性を確保するための必要条件は、単位の時間ステップ
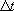 だけ経過したときの波面の進行距離が単位のグリッド内におさまるという条件である。この場合、グリッド間隔 だけ経過したときの波面の進行距離が単位のグリッド内におさまるという条件である。この場合、グリッド間隔
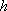 の等間隔グリッドを用いた三次元差分方程式では、最速波の速度を の等間隔グリッドを用いた三次元差分方程式では、最速波の速度を 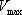 とすると時間ステップ とすると時間ステップ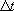 は以下の条件を満足しなければならない(Graves、1996)。 は以下の条件を満足しなければならない(Graves、1996)。
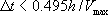 (4.2−1) (4.2−1)
(3) 吸収境界条件
計算機の能力に限界があることから、有限差分法でモデル化できる媒質の範囲(計算領域)は限られる。計算領域の境界面に何らの境界条件も与えないとこれらの面は剛体壁(固定端)として振る舞うため、この面に達した波は完全反射して計算領域内に戻ってきてしまう。しかし、実際の地盤にこのような壁は存在しない。この計算上の反射波を防ぐには、十分大きな計算領域を設定し、反射波が着目地点に戻ってくる前に計算を打ち切る必要がある。しかし、この方法では計算する地震波の継続時間が長ければ長いほど計算領域を大きくとらなければならなくなり、記憶容量、計算時間とも膨大になってしまう。そこで、計算領域を必要以上に大きくとらない方法として、境界面に入射した波が吸収される吸収境界条件(absorbing boundary condition)が開発された。この吸収境界条件としてはClayton and Engquist(1977)のものが有名であるが、この吸収境界条件だけでは反射波の抑止が完全ではない。そこで最近では、境界面から20 あるいは30 点の格子点を帯状の波動吸収領域として用い、この中では時間ステップ毎に波の振幅に指数関数を乗じ振幅を徐々に減少させる方法(Cerjan et al., 1985)が用いられている。Graves(1996)、Pitarka(1999)の有限差分法では、Clayton and Engquist(1977)の吸収境界条件とCerjan et al.(1985)の帯状の吸収領域が併用されている。
(4) 地表面における応力解放条件
直交格子を基本とする有限差分法で地表面における応力解放条件を満足させ、かつ数値安定性を確保することはそう簡単ではない。有限差分法で地表面を扱う方法の一つは自由地表面での応力零の条件を陽に定式化する方法である(Zero
- stress formulation)。地表面が水平な場合には場の逆対称性を利用して応力零の条件を満足するために必要な地表面上および地表面より上の空中の格子点の変位や応力の値を容易に計算できる(例えば、Levander,
1988; Graves, 1996; Pitarka, 1999)。この場合には数値的な安定性が確保され精度もよい。しかし、この方法を凹凸がある地表面に適用することは難しい。
(5) 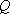 値 値
媒質の一般的な非弾性減衰を考慮するには応力と歪みとのコンボリュ-ションの操作が必要となるため単純な陽解法を維持できなくなり、計算に必要な記憶容量や計算時間が格段に増大する(例えば、Emmerichand Korn, 1987)。そのため、これまでの有限差分法の計算では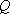 値の効果を無視する場合が多い(例えば、Yomogida and Etgen, 1993; Olsen
and Archuleta, 1996)。最近、近似的扱いにより陽解法を維持したまま空間的に変化する 値の効果を無視する場合が多い(例えば、Yomogida and Etgen, 1993; Olsen
and Archuleta, 1996)。最近、近似的扱いにより陽解法を維持したまま空間的に変化する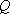 値の効果を有限差分法に導入するテクニックが提案され、その有効性の確認が行われている(Graves,
1996)。このテクニックでは、限られた帯域波の計算を前提に非弾性減衰による位相速度の分散性を無視し、P波とS波の 値の効果を有限差分法に導入するテクニックが提案され、その有効性の確認が行われている(Graves,
1996)。このテクニックでは、限られた帯域波の計算を前提に非弾性減衰による位相速度の分散性を無視し、P波とS波の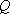 値を区別せずに周波数に比例する 値を区別せずに周波数に比例する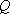 値を仮定することで、各時間ステップの速度場および応力場に指数関数型の減衰項を乗じる操作を施す。強震記録から推定された 値を仮定することで、各時間ステップの速度場および応力場に指数関数型の減衰項を乗じる操作を施す。強震記録から推定された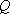 値に関する多くの既往の研究では 値に関する多くの既往の研究では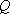 値が周波数にほぼ比例する結果となっている。これらの研究で用いた記録の分解能からは約1Hz
よりも低周波数帯域で 値が周波数にほぼ比例する結果となっている。これらの研究で用いた記録の分解能からは約1Hz
よりも低周波数帯域で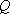 値が周波数に比例するのかどうか定かではないが、約1Hz より高周波数帯域の観測結果に基づけば、Graves(1996)の周波数比例の 値が周波数に比例するのかどうか定かではないが、約1Hz より高周波数帯域の観測結果に基づけば、Graves(1996)の周波数比例の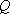 値の仮定は不自然ではない。ただし、この方法ではP波とS波の 値の仮定は不自然ではない。ただし、この方法ではP波とS波の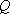 値を区別できない。 値を区別できない。
C. 震源のモデル化
断層面上の滑り時間関数や破壊時刻といった運動学的パラメターを先験的に与える運動学的断層モデルの場合、有限差分法のような領域法に属する離散化手法で最も問題なのは、一つの格子点にダブルカップルを厳密に作用させるのが簡単ではないことにある。この問題点の解決法として、分布震源を用いる方法とソースボックス法の二通りがある(竹中,
1993)。前者は有限な広さを持つ複数の格子点にそれぞれ異なった向きのシングルフォースを作用させることで分布震源としてダブルカップルを近似的に表現する方法である(Aboudi,
1971)。この方法は簡便なことからよく用いられてきた(例えば、Frankel, 1993)。最近、Graves(1996)はこの方法と食い違い格子(スタッガードグリッド)との取り合わせがよいことに着目し、三次元場の食い違い格子におけるモーメントテンソルの表現式を導いている。Pitarka
et al.(1999)でもGraves(1996)と同様の方法でダブルカップルの点震源をモデル化している。
D. 不等間隔格子による有限差分法
本検討では、不等間隔格子を用いたPitarka(1999)の有限差分法により計算を行う。不等間隔格子の模式図を図4.2−2に示す。有限差分法による計算を行う際には、計算の対象とする媒体を直方体の格子点に離散化する。この時、計算の安定条件を満たすために、格子間隔は(4.2−1)式と次の条件を満たす必要がある。
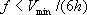 (4.2−2) (4.2−2)
ここで、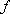 は計算したい最大周波数(Hz)、 は計算したい最大周波数(Hz)、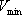 (km/s)はモデル内の媒質の伝播速度のうち最も遅い速度、 (km/s)はモデル内の媒質の伝播速度のうち最も遅い速度、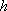 (km)は最小格子間隔である。 (km)は最小格子間隔である。
また、用いる格子点数はすなわち必要とする計算機のメモリ量となるため、同じメモリ量を使用できる場合はより大きな領域を計算できる。
以上の理由により三次元盆地構造を考慮した地震動の計算に不等間隔格子による有限差分法を用いた。
E. 三次元有限差分法に用いる計算用地盤モデル
「3. 地下構造モデルの設定」に基づき、三次元有限差分法に用いる計算用三次元地盤モデルを作成した。
三次元有限差分法では、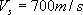 の層を上面とした地下構造モデルで計算を行う。 の層を上面とした地下構造モデルで計算を行う。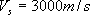 の地震基盤から の地震基盤から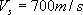 の層までの物性値を表4.2−1 に示す。 の層までの物性値を表4.2−1 に示す。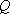 値以外の物性値は、既に「3. 地下構造モデルの設定」の中で設定されている。 値以外の物性値は、既に「3. 地下構造モデルの設定」の中で設定されている。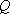 値は、1、2 層目はSatoh et al.(2001)が仙台市直下のM5.0 の地震の強震動を三次元差分法でシミュレーションしたときに用いた 値は、1、2 層目はSatoh et al.(2001)が仙台市直下のM5.0 の地震の強震動を三次元差分法でシミュレーションしたときに用いた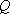 であり、3層目は、Yamanaka and Kikuchi(2002)が1978 年宮城県沖地震のインバージョンに用いた であり、3層目は、Yamanaka and Kikuchi(2002)が1978 年宮城県沖地震のインバージョンに用いた である。 である。
「3. 地下構造モデルの設定」に基づき作成したA1 断層に対する計算領域での三次元地盤モデルを図4.2−3 に、A2 断層に対する三次元地盤モデルを図4.2−4 に示す。両図のコンターは、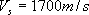 層の上面の深さ分布である。各図には、沈みこむプレートの上面を濃いオレンジ色で表示した。なお、位置関係を明確にするために、各図にはK-NET
観測点の位置も表示した。仙台市中心部に近い観測点は図中の SEN であり、KNET
観測点名は仙台(MYG0013)である。 層の上面の深さ分布である。各図には、沈みこむプレートの上面を濃いオレンジ色で表示した。なお、位置関係を明確にするために、各図にはK-NET
観測点の位置も表示した。仙台市中心部に近い観測点は図中の SEN であり、KNET
観測点名は仙台(MYG0013)である。
F. 三次元有限差分法による計算条件
仙台平野の最も堆積層が厚い地点での1次卓越周期は3.5秒程度、仙台の市街地での1次卓越周期は2.0〜3.0秒程度と推定されている(佐藤・他,
1998; Satoh et al., 2001)。したがって、仙台の市街地での1次卓越周期の増幅特性を評価するためには、少なくとも1.5秒程度まで三次元有限差分法で計算できることが望ましい。このような条件と計算機の性能を考慮して、以下の条件で計算を実施することとした。
・グリッド
・グリッド数
・最小グリッド間隔
・出力点総数
・出力波継続時間
・出力波時間刻み |
1231×647×105
83,627,985
0.15km
10,200
250 秒
0.05 秒 |
なお、深さ方向のグリッド間隔は以下の通りである
・0〜3km
・3〜6km
・6〜12km
・12〜60km |
0.15km
0.30km
0.6km
0.75km |
領域内の最小弾性波速度700m/sと最小グリッド間隔0.15kmを用いると(4.2−2)式により1.3秒までの計算を精度よく行うことが可能である。このような理由から、後述するハイブリッド法によるマッチングフィルターの中心周期を1.5秒としている。
|