5. その他の検討
5.1 距離減衰式のばらつきに関する検討
5.1.1 距離減衰式のばらつきに関する検討課題
西日本を対象とした確率論的地震動予測地図試作版の審議過程において、
距離減衰式のばらつきの値(自然対数標準偏差で0.53)は過大ではないか?
この中には、サイト特性や伝播経路特性に起因するものなど、対象地震と地点が決まれば本来は確定的に扱えるものも含まれている。これらは分離して扱うべきであり、ハザードカーブの計算ではランダムなもののみを考慮すべきはないか?
との指摘がなされた。これは、
確率論的な地震ハザード評価では、本来、「地震(場所と規模)」と「評価地点」が固定された場合の地震動のばらつきが必要である。
しかし、実際に用いられているのは、「多数の地震」による「多数の地点」での観測記録に基づくばらつきであり、本来用いるべきものとは異なるものである。これは、ばらつきを過大評価していることになるのではないか。
と言い換えることもできる。同様の指摘は、Anderson and Brune(1999)によってもなされている。
距離減衰式のばらつきについては、最終的には「確率論的地震動予測地図の作成に用いる値をいくつにするか」を決める必要があるが、それを判断する上で直接的に関連する主な課題・論点を分類すると、以下のようになる。
- 対数正規分布の妥当性
- 地震動強さの上限値設定
- ばらつきの種類(認識論的不確定性と偶然的不確定性)による分離と値の設定
- ばらつきの振幅依存性
- 分布の裾の打ち切り
このうち、1. の対数正規分布の妥当性については、観測記録のばらつきの分布形状から、ある程度の範囲ではほぼ成立していると考えられるものの、分布の裾を考えるのであれば、他の分布の適用の可能性などを含めてより詳細に検討すべきとの考えから、長期的な課題として、今回の検討の対象外とした。
また、2. の地震動強さの上限値についても、無限大の地動を認めることが適切でないことは共通認識となっているものの上限値そのものを設定することは、現時点の知見では容易ではないとの考えから、やはり長期的な課題として今回の検討の対象外とした。
以下では、距離減衰式に含まれるばらつきの分類とその取り扱い、2003年十勝沖地震の本震・余震の記録に基づくばらつきの値、ばらつきの振幅依存性、および分布の裾の打ち切りについて、それぞれ検討した結果を示す。
5.1.2 ばらつきの分類と分離
(1)認識論的不確定性と偶然的不確定性
ばらつき・不確定性を、「認識論的不確定性(Epistemic Uncertainty)」と「偶然的不確定性(Aleatory Uncertainty)」に分けて取り扱う方法は、米国における原子力施設の地震PSAで採用されている。両者の分離には任意性があり、前者を「知識不足に起因するもの」と定義すると、「突き詰めればほぼ全てが認識論的不確定性に分類されるのではないか?」との考えもあるが、US NRC (2002)では、
- ●認識論的不確定性:
- 本来一つの値に決まるべきパラメータが、データ不足によって決められないことに起因するもの。データの増加に伴って減少する。
- ●偶然的不確定性:
- データが増えても減少させることができない種類の不確定性で、採用しているモデル自体の現象説明能力が不十分であることに起因するものもここに含む。
としている。つまり、両者の分類は用いるモデルに依存し、ひいては時代とともに変化することになる。
(2)ばらつきの成因による分類
-
震源・伝播経路・サイト
「一つの地震に対する一つの地点における地震動強さのばらつき」を知るためには、現在の距離減衰式のばらつきを、震源特性、伝播経路特性、サイト特性それぞれの不確定性に起因するものに分けて考える必要がある。例えば、以下のように考えることができる。
- 現状の距離減衰式のばらつきには、サイト特性の推定誤差に関わるものが含まれている。これは、観測記録に基づいて地点特性が評価できれば減少させることができるものであるから、定量化した上で排除すべきではないか。
- 地震と地点が固定されると、伝播経路特性とサイト特性のばらつきのうちランダムなものは無視できるはずなので、震源特性の不確定性のみを抽出して考慮すればよいのではないか。
現実には、ばらつきを個々の要因ごとに分離することは困難と考えられるが、間接的な評価を試みた例はいくつかある。
-
地震間のばらつきと地震内のばらつき
距離減衰式を導出する際に、ばらつきを「地震間のばらつき」と「地震内のばらつき」とに分離することが可能である。近年の距離減衰式では、式のばらつきとして全体のばらつきとともに両者に分離した数値が出されている場合も見受けられる。
直感的には、「地震間のばらつき」には震源特性に起因するばらつきが、「地震内のばらつき」には伝播経路特性とサイト特性に起因するばらつきが、それぞれ強く関与しているように思われるが、震源特性に起因するものの中には、「地震内」に影響するものもあるなど、必ずしも明確に対応付けられるものではない。
距離減衰式に関する既往の研究成果では、ばらつきの値は、常用対数の標準偏差で以下のようになっている。ただし、地震動強さの指標、式の説明能力、サイト特性の取扱い、使用データなどがそれぞれ異なっており、比較の際には注意が必要である。
- トータルのばらつきは、
サイト補正なし:0.3程度以上
簡便なサイト補正:0.22〜0.3程度
観測記録でサイト補正:0.2〜0.27程度
- 地震間と地震内のばらつきは、地震間:0.1〜0.18、地震内:0.2〜0.24。
- 震源特性のばらつきは0.16〜0.2程度。
- 伝播経路特性のばらつきは0.1〜0.2程度。
- サイト特性のばらつきは0.2程度。
(3)ばらつきの取扱いの方針
全国を対象とした確率論的地震動予測地図の作成では、距離減衰式のばらつきの取り扱いについて、以下の方針を設定した。
- 地震ハザード評価では、それぞれの地点での地震動の強さのばらつきが必要である。これに対して、距離減衰式を作成する際に得られる回帰のばらつきは、異なる地点が混在することに起因するものが含まれる。したがって、そのばらつきは、本来、ハザードカーブの算定にそのまま流用して用いるべきものでないと考えられる。そこで、異なる地点が混在することの影響を除去したばらつきを算出する。
- 確率論的地震動予測地図の作成で用いる地震動評価の手法は、司・翠川の式で推定される最大速度とそれに対する相対的なサイト特性から地表面での最大速度を推定するものである。モデルとしてはサイト固有の特性を説明する能力を有するが、データ不足の(全メッシュで利用可能なデータは国土数値情報しかない)ためにサイト特性の推定誤差(下記3)
でいうところの認識論的不確定性に分類される)が含まれることから、これに該当するばらつきを分離・除去する。
- 以上のことは、ばらつきの種類分けの視点からは、ハザードカーブの計算には地震動評価にかかわる偶然的不確定性のみを考慮し、認識論的不確定性は含めない、となる。ここで、偶然的不確定性には、評価モデルの現象説明能力が不十分であることに起因するものも含まれる。ちなみに、地震活動のモデルでは、例えば
- 主要98断層帯では長期評価に基づく最大規模の地震が発生するとしている。
- 主要98断層帯の平均活動間隔や最新活動時期に幅がある場合に、その中央の値を用いている。
- 南海トラフの地震の発生様式として、1つのモデルを設定している。
- 震源断層を予め特定しにくい地震の発生頻度として、地域区分の有無と地震カタログの違いによる合計4ケースの平均値を用いている。
といった取扱いがされており、それぞれの設定にかかわる認識論的不確定性はハザードカーブの計算には考慮されていない。(また、不確定性そのものも定量化されていない)
- ハザードカーブの算定に用いるばらつきの値は、既往の研究成果ならびにここで実施する検討結果に基づき設定する。
5.1.3 十勝沖地震の本震・余震に基づく検討
地震動の評価におけるばらつきを要因別に分離するために、2003年十勝沖地震の本震と余震における防災科研のK-NET, KiK-netの記録を用いて、
- サイト特性の評価と地点ごとのばらつきの評価
- サイト特性を除去した後に残るばらつきの評価
を実施した。ほぼ同一の領域で発生した地震のデータを用いたのは、様々な領域で発生する地震のデータを用いる場合と比較して、震源特性と伝播経路特性に関するばらつきの影響を少なくする効果があり、地震と地点とが固定された場合のばらつきの値に多少なりとも近づけることができると考えたためである。ただし、現在の評価手法を用いる限りにおいては、震源特性や伝播経路特性に起因するばらつきを減少させることはできないことに注意が必要である。
(1)データ
- 2003年9月26日に発生した十勝沖地震の本震と、2004年2月までに発生した余震のうちM5.0以上のもの、合計45地震。余震は、震源位置で判断(図5.1-1)。
- 火山フロントよりも南東にあるK-NET, KiK-net の観測点で、これらのうち10地震以上が観測されている76地点を選定(図5.1-1)。
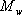 = = 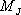 と仮定。 と仮定。
- 断層面の広がりは、本震および最大余震のみ考慮し、その他は点震源を仮定して断層面までの最短距離を評価。
(2)記録の処理
- 観測記録に対して、司・翠川 (1999) と同様のフィルタ処理を施し、水平2成分の最大速度のうち大きい方を採用。
- 国土数値情報による増幅率は、藤本・翠川 (2003) に基づき評価したものを使用。
- 北日本の太平洋プレートの地震に対する補正は考慮せず。
(3)検討の手順
- 地震
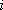 による地点 による地点 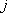 での観測記録 での観測記録 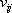 について、司・翠川の式で推定される最大速度 について、司・翠川の式で推定される最大速度 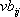 に対する比 に対する比 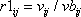 を評価。 を評価。
- この結果を地点ごとに整理し、サイト係数
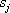 を地点ごとの比 を地点ごとの比 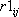 の相乗平均値として推定。あわせて の相乗平均値として推定。あわせて 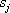 のまわりのばらつき(常用対数の標準偏差で表示、以下同様)を評価。 のまわりのばらつき(常用対数の標準偏差で表示、以下同様)を評価。
- 国土数値情報による増幅率
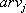 を考慮した式に対する比 を考慮した式に対する比 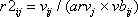 についても同様にサイト係数 についても同様にサイト係数 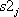 とばらつきを評価。 とばらつきを評価。
- KiK-net の観測点については、
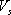 30(地表から地下30mまでの平均S波速度)に基づく補正を考慮した場合について、同様の評価を実施。 30(地表から地下30mまでの平均S波速度)に基づく補正を考慮した場合について、同様の評価を実施。
- 観測値と推定値の比
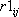 を地震ごとに整理し、地震ごとの特性 を地震ごとに整理し、地震ごとの特性 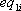 を を 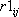 の地震ごとの相乗平均値として推定。あわせてばらつきも評価。 の地震ごとの相乗平均値として推定。あわせてばらつきも評価。
- 地点ごとに国土数値情報による増幅率を考慮した場合、
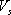 30に基づく補正を考慮した場合、および観測記録に基づき推定されたサイト係数を考慮した場合についても同様に地震ごとの特性とばらつきを評価。 30に基づく補正を考慮した場合、および観測記録に基づき推定されたサイト係数を考慮した場合についても同様に地震ごとの特性とばらつきを評価。
(4)結果
- 地点ごとに整理した観測値と推定値の比(図5.1-2)
- 地点による特性の違いが大きいことがわかる。
- 地点ごとのばらつきには変動があるものの、常用対数の標準偏差で0.15〜0.3程度の範囲にあり、平均的には0.22程度となっている(ただし、この値には地点ごとのデータ数の重みは考慮されていない)。
- 工学的基盤の式に対するサイト係数の平均値は0.99、サイト係数自体の平均値まわりのばらつきは0.23程度である。
- 今回のデータが同一震源域のものであることから、サイト係数の絶対値には震源域に固有の特性や伝播経路特性の分も含まれていると考えられる。
- 地震ごとのばらつき(図5.1-3)
- 地震ごとの特性のばらつきは、中段の●のばらつきから0.11程度である。この値は、既出文献での値よりも有意に小さいが、同一震源域で発生した地震のみを対象としていることに起因している可能性がある。
- サイト補正の方法によるばらつきの変化(図5.1-4、図5.1-5)
- K-NET, KiK-netのデータを両方用いた場合(図5.1-4)には、ばらつきの値は、
0.30(補正なし)→0.28(国土数値情報で補正)→0.21(観測記録で補正)
となる。この0.21と、a. の0.22の違いは、地点ごとのデータ数の重みの有無によると考えられる。
- サイト特性の推定に関わるばらつきが、他のばらつきと独立であると仮定すると、国土数値情報からサイト係数を推定する際の推定誤差は、
となる。この数値は、サイト係数のばらつき(図5.1-2の中段)よりもやや小さいが、この違いは、地点ごとのデータ数の重みの有無に起因すると考えられる。
- ・KiK-netのデータだけ(図5.1-5)で見ると、ばらつきの値は、
0.31(補正なし)→0.29(国土数値情報で補正)→
→0.26(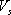 30で補正)→0.21(観測記録で補正) 30で補正)→0.21(観測記録で補正)
となり、全データの場合とほぼ同様である。
- 全データの場合と同様に、サイト係数の推定誤差を出すと、以下のようになる。
国土数値情報から推定: 0.19(約1.5倍/1.5分の1)
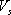 30から推定: 0.15(約1.4倍/1.4分の1) 30から推定: 0.15(約1.4倍/1.4分の1)
- 特異な震度分布を示す2地震のデータを除去した結果(図5.1-6、図5.1-7)
- 震度分布が震央に対して特定の方角でのみ大きい傾向を示す2003年9月26日06時08分の最大余震および2003年9月27日17時06分の地震を除去したデータを用いて、上記のc.
と同様の分析を行った。図5.1-8には、最大余震の最大加速度の分布を示すが、震央に対して北西方向で地動が大きいことがわかる。
- K-NET, KiK-netのデータを両方用いた場合(図5.1-6)には、ばらつきの値は、
0.29(補正なし)→0.27(国土数値情報で補正)→0.19(観測記録で補正)
となる。
- KiK-netのデータ(図5.1-7)で見ると、ばらつきの値は、
0.30(補正なし)→0.27(国土数値情報で補正)→
→0.26(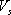 30で補正)→0.20(観測記録で補正) 30で補正)→0.20(観測記録で補正)
となり、全データの場合とほぼ同様である。
- c. の場合と比較して、ばらつきの値が若干減少しており、観測記録による補正後の値が、K-NET+KiK-netの場合には0.21→0.19、KiK-netのみの場合には0.21→0.20となっている。
(5)十勝沖地震の本震・余震記録に基づくばらつきの値のまとめ
- サイト特性の推定に関わる不確定性は「認識論的不確定性」に分類することができると考えられることから、この不確定性を除去した場合の距離減衰式のばらつきを評価すると、全てのデータを用いた場合には常用対数標準偏差で約0.21、特異な震度分布を示す2地震を除いた場合には0.19〜0.20となった。
- 国土数値情報に基づきサイト係数を推定する際のばらつき(認識論的不確定性)は、常用対数標準偏差で0.19程度となった。
5.1.4 ばらつきの振幅依存性、規模依存性、距離依存性
5.1.3で用いた2003年十勝沖地震の本震と余震のデータを用いて、ばらつきの振幅依存性、規模依存性、および距離依存性の有無を調べた。
(1)ばらつきの振幅依存性(図5.1-10)
- サイト補正をしない場合にはばらつきの値は振幅によらず0.3程度でほぼ一定値となる。
- サイト補正後は、全体では約0.2程度であるが、速度振幅が2〜5cm/s付近で一旦ばらつきが増加し、10cm/s以上では0.2をやや下回る。ただし、速度振幅が2cm/s以上のデータは数が少ないため、ばらつきの値の変化が本質的なものかデータが少ないことによるものかの判断はできない。なお、特異な震度分布を示す2地震を除去した場合には2〜5cm/s付近の値が幾分減少する。
- 翠川・大竹(2003)による検討(図5.1-9)によれば、最大速度のばらつきには明らかな振幅依存性が認められている。ただし、ばらつきが0.2より小さくなるのは、推定最大速度が15〜20cm/sを超えてからであるが、本検討では、この範囲のデータが少なく、大振幅でのばらつきの振幅依存性を議論するには不十分である。
- 翠川・大竹(2003)では、振幅が5cm/s以下の領域でばらつきが大きい傾向が示されているが、本検討の結果ではそのような傾向が見られない。この理由として、対象としたデータの震源域とサイトとが限定されているためだと推測される。
(2)ばらつきの規模依存性(図5.1-11)
- サイト補正の有無に関わらず、マグニチュードが大きいところでばらつきが大きい傾向が見られる。ただし、マグニチュードが7.0以上の地震は本震と最大余震のみであり、最大余震でばらつきが大きいことが主たる原因と推測される。
(3)ばらつきの距離依存性(図5.1-12)
- サイト補正の有無に関わらず、ばらつきの値は、距離によらず概ね一定値である。50km以内ではばらつきがやや小さいようにも見えるが、データ数がごく少ないことに注意を要する。
(4)ばらつきの振幅・規模・距離依存性に関するまとめ
- ばらつきの振幅依存性は、(1)に基づき、暫定的な取扱いとして図2.7-1のように設定する。
- ばらつきの規模依存性、距離依存性については考慮しない。
5.1.5 分布の裾の打ち切り
5.1.3で検討の対象とした十勝沖地震の本・余震のデータでは、観測記録によるサイト補正後のばらつきが常用対数標準偏差で0.2117となっている。これより、
- ±1σの範囲 0.614倍(1.63分の1)〜1.63倍
- ±2σの範囲 0.377倍(2.65分の1)〜2.65倍
- ±3σの範囲 0.232倍(4.31分の1)〜4.31倍
であるが、図5.1-13より、±2σはもとより±3σの範囲を超えるデータも散見されることがわかる。
参考までに、
- 平均+1.0σを超える確率=16%、平均+1.5σを超える確率=6.7%、
- 平均+2.0σを超える確率=2.3%、平均+2.5σを超える確率=0.63%、
- 平均+3.0σを超える確率=0.14%
となるため、50年間の超過確率5%、あるいは30年間の超過確率3%といった確率レベルまでを対象とする場合に(その期間内で100%に近い発生確率の地震があるとしても)結果に相当の影響を及ぼすと考えられるのは、+2σ程度以内の範囲であると言える。このことから、観測記録からは±3σの範囲を超えるデータも存在するが、全国を対象とした確率論的地震動予測地図で対象とする確率レベルが比較的高いことを勘案して、±3σの範囲を超えるデータを統計的な異常値とみなし、対数正規分布の裾を打ち切ることとする。
5.1の参考文献
- Anderson, J.G. and J.N. Brune (1999): Probabilistic Seismic Hazard Analysis without the Ergodic Assumption, Seismological Research Letters, Vol. 70, No. 1, pp. 19-28.
- 藤本一雄・翠川三郎(2003):日本全国を対象とした国土数値情報に基づく地盤の平均S波速度分布の推定, 日本地震工学会論文集, 第3巻, 第3号, pp.13-27.
- 翠川三郎・大竹雄(2003):地震動強さの距離減衰式にみられるバラツキに関する基礎的分析, 日本地震工学会論文集, 第3巻, 第1号, pp.59-70.
- 司宏俊・翠川三郎(1999):断層タイプ及び地盤条件を考慮した最大加速度・最大速度の距離減衰式, 日本建築学会構造系論文報告集, 第523号, pp.63-70.
- U.S. Nuclear Regulatory Commission (2002): Guidance for Performing Probabilistic Seismic Hazard Aalysis for a Nuclear Plant Site: Example Application to the Southeastern United Steates, NUREG/CR-6607.
|