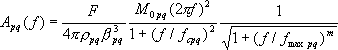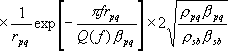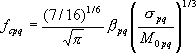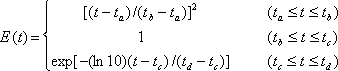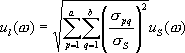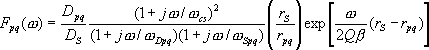5.2.2　統計的グリーン関数法

　壇・佐藤による統計的グリーン関数法(1998)は、断層面を小断層に分割し、小断層ごとにBooreの統計的震源モデル(1983)を分布させ、Irikuraの方法(1986)でモデルに従うように重ね合わせる方法に準拠するが、断層の非一様すべりを破壊モデルを規定する量のうち、低振動数の地震波の放出量に対応する非一様すべり量と高震動数の地震波の放出量に対応する非一様すべり量とを考慮した合成方法である。小地震波である半経験的グリーン関数が使用できない場合にも使用できるが、位相をランダムと仮定しており、特に短周期で有効な方法である。

　①　統計的グリーン関数（加速度フーリエスペクトル）の作成

　断層の食い違い理論(Aki and Richards,1980)によれば、無限媒質のときの遠方場におけるS波の変位波形は、

(5-7)

と表される。ここに、はS波の放射特性(radiation pattern)、は媒質の密度、は媒質のS波速度、は震源距離、を断層面上の点、は断層面上の点におけるすべり速度時間関数、は断層面である。本文では、(5-7)式の(5-8)式に相当する部分を震源時間関数部といい、そのフーリエ変換を震源スペクトルと呼ぶ。

(5-8)

　今、すべり速度時間関数が、断層面上でによらず同形とすると、点が破壊する時刻をとして、(5-8)式は下のように書くことができる。

(5-9)

　以上により地震基盤におけるS波の主要動の統計的グリーン関数をBoore(1983)の統計モデルに準拠して作成した。この統計モデルは、

(5-10)

で表される地震動の加速度フーリエスペクトルのモデルである。
　ここに、は要素断層に関する添え字で、は地震動の加速度フーリエスペクトル、は地震動の放射特性、およびは要素断層における地殻の密度およびせん断波速度、は地震モーメント、は臨界振動数、は高周波遮断振動数、は定数、は震源距離、は地殻の値、およびは地震基盤の密度およびせん断波速度である。最終項は、自由表面の影響および要素断層における地殻のインピーダンスと地震基盤のインピーダンスとの比較との相違を考慮したものである。
　また、震源の大きさに関する量であるおよびについては、以下の式で求める。

(5-11)

ここに (= )は地殻の剛性率、は実効応力である。

　② 　時刻歴（統計的経時特性）の作成

　時刻歴の作成には経時特性もしくは位相特性が必要であるが、地震基盤におけるS波の主要動の経時特性に関しては、現在までに研究があまりされていない。このプログラムでは、最終的に統計的グリーン関数を定義する位置を工学的基盤上と考え、気象庁マグニチュードと震源距離とで規定される佐藤・他(1994a)による仙台地域の工学的基盤におけるS波の主要動の地震記録から求められた統計的経時特性を準用している。

経時特性の式は以下の式で表される。

(5-12)

ここで、

である。気象庁マグニチュードは、佐藤(1989)による式で地震モーメントより(5-13)で計算する。

(5-13)

　③　要素地震波形（種地震）の作成

　①および②の結果より要素地震波形（種地震）を作成する。種地震の作成は①で作成した加速度フーリエスペクトルにランダムな位相を与え(理論的なスペクトルに[- , ]の一様な乱数で位相を与える)、ランダムな位相を与えた後の処理は以下の通り。

与えたフーリエ振幅と乱数位相で、フーリエ逆変換を行って、時刻歴を作成する。
この時刻歴に（時間領域で）統計的経時特性をかける。フーリエ変換をして、位相情報を残す。（振幅の情報は捨てる。）
再度、与えた加速度フーリエ振幅と残しておいた位相で、フーリエ逆変換を行って、時刻歴を作成する。
結果、位相情報を変化させないようにエンベロープ処理を行う。

図5.2にランダムな位相を与えた種地震（要素地震）波形例を示す。

本検討で用いた種地震作成パラメータを表5.1に示す。

　④ 波形合成法（統計的グリーン関数法）アルゴリズム

●壇・佐藤(1998)の方法

　壇・佐藤(1998)は、断層の非一様すべり破壊モデルを規定する量のうち、低振動数の地震波の放出量に対応する非一様すべりと高振動数の地震波の放出量に対応する非一様すべり速度とを考慮した合成方法を提案した。壇・佐藤(1998)の合成方法は、大地震の( , )番目の要素断層の震源スペクトルおよび小地震の震源スペクトルを下式のように変更したものである。

(5-14)

ここに、大地震の要素断層の大きさと小地震の大きさは等しいとしている( = ) 。また、は虚数単位、は小地震の臨界円振動数で、は媒質のせん断剛性率、は媒質のS波速度、は実効応力、は要素断層を面積が等価な円としたときの半径である。上の大地震の( , )番目の要素断層の震源スペクトルと小地震の震源スペクトルとの比率をとると、スケールファクターは、

(5-15)

となる。壇・佐藤(1998)の合成方法によって得られる合成波形のフーリエ変換の低振動数領域および高振動数領域における振幅は、距離補正項を無視すると、

	( →　0 )	(5-16)
	( →　∞ )	(5-16)

となる。ただし、高振動数領域における振幅はランダム和となることを考慮した。ここで非一様な実効応力が全ての要素断層においてに等しいとして、小地震の実効応力に対する比率をと等しいとして、小地震のすべり量に対する比率をとおくと、

	( →　0 )	(5-17)
	( →　∞ )	(5-17)

となる。さらに小地震と大地震との間で巨視的断層パラメータの相似則が成り立っていると仮定すると、

	( →　0 )	(5-18)
	( →　∞ )	(5-18)

となる。

　壇・佐藤(1998)は、この合成方法を、Wald and Somerville(1995)が測地データと周期４秒以上地震記録から同定した。計算の対象としている周期は0.067秒～4秒であり、やや短周期帯域の地震動を主体にしている。壇・佐藤(1998)は、これらの合成波形より算定した計測震度は、報告されている気象庁の震度と良く対応した値となって強震動の予測問題という観点から、断層の非一様すべり破壊モデルによる結果を、従来の巨視的断層モデルおよび次式で定義される断層面全体の短周期レベルが非一様すべり破壊モデルと等しくなるような等価一様すべり破壊モデルの２つを考え、３つのモデルによる合成結果を相互比較した。

(5-19)

　以上の結果より断層近傍の館山を除く５地点で、非一様すべり破壊モデルによる合成結果と等価一様すべり破壊モデルによる合成結果はほぼ同じとなり、従来の巨視的断層モデルによる合成結果はやや小さくなった。以上より距離補正項を入れたスケールファクターの式を以下に示す。

(5-20)


←　Back	Next　→

5.2.2 統計的グリーン関数法

　5.2.2　統計的グリーン関数法