5.4. すべり速度時間関数の設定
選定されたケース3 の断層パラメータを用いて、三次元有限差分法に用いるすべり速度時間関数を中村・宮武(2000)の方法により算定した。中村・宮武(2000)のすべり速度時間関数の近似式を計算するためには以下のパラメータが必要となる。それぞれのパラメータを求めるために与えるべき定数は、震源スペクトルから見積もられる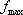 (source-controlled (source-controlled 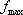 )、すべり時に働く動的な応力降下量 )、すべり時に働く動的な応力降下量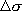 、断層幅 、断層幅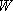 、ローパスフィルターのコーナー周波数 、ローパスフィルターのコーナー周波数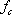 (sourcecontrolled (sourcecontrolled 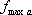 と同等)、破壊速度 と同等)、破壊速度 、剛性率 、剛性率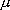 、最終すべり量 、最終すべり量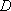 の計6 つである。 の計6 つである。
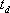 (最大すべり速度到達時間) (最大すべり速度到達時間)
震源スペクトルから見積もられる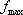 (source-controlled (source-controlled 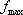 )との関係(中村・宮武(2000)の(9)式)から求める。 )との関係(中村・宮武(2000)の(9)式)から求める。
( 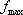 に反比例) に反比例)
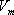 (最大すべり速度) (最大すべり速度)
すべり時に働く動的な応力降下量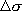 、断層幅 、断層幅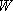 、ローパスフィルターのコーナー周波数 、ローパスフィルターのコーナー周波数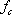 (source-controlled fmaxaと同等)、破壊速度 (source-controlled fmaxaと同等)、破壊速度 、剛性率 、剛性率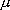 との関係(中村・宮武(2000)の(10)式の誤植を下式のように修正)から求める。 との関係(中村・宮武(2000)の(10)式の誤植を下式のように修正)から求める。
( 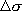 に比例 に比例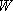 、 、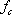 、 、 の平方根に比例、 の平方根に比例、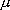 に反比例) に反比例)
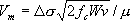 (5.4−1) (5.4−1)
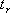 (ライズタイム) (ライズタイム)
断層幅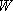 と破壊伝播速度 と破壊伝播速度 を用いて近似式から求める。 を用いて近似式から求める。
( 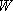 に比例、 に比例、 に反比例) に反比例)
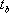 (すべり速度振幅が (すべり速度振幅が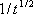 に比例するKosttov 型関数に移行する時間) に比例するKosttov 型関数に移行する時間)
すべり速度時間関数の近似式(中村・宮武(2000)の(7)式)で最終すべり量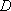 を与えることにより自動的に求めることができる。 を与えることにより自動的に求めることができる。
以上のような考え方で設定した、A1 断層、A2 断層に対するすべり速度時間関数のパラメータを、それぞれ、表5.4−1、表5.4−2 に示す。また、A1 断層、A2 断層に対するすべり速度時間関数を、それぞれ、図5.4−1、図5.4−2 に示す。実際の計算では、すべり速度時間関数を三角パルスの重ね合わせで近似して与えるため、図5.4−1、図5.4−2 には中村・宮武(2000)に基づくすべり速度時間関数の他、計算用のすべり速度時間関数を表示した。
|