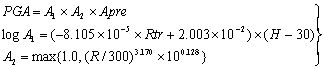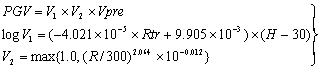2.4.2 距離減衰式の補正項の検討A. 検討の背景今回の試作版の対象である北日本地域では、震源の深さが60kmよりも深いやや深発地震の活動が活発であり、1993年釧路沖地震(気象庁マグニチュード7.8)のように、震源の深さが100km程度であっても被害が生じた地震も発生している。やや深発地震では、震源距離が同じであっても、日本海側の地域よりも太平洋側の地域において地震動が大きくなる異常震域が現れることが知られている。この現象は、図2.4.2-1のようなプレートの沈み込み帯における特異な地震波の減衰(Q)構造によって説明されている(例えば、宇津,1977)。しかしながら、現在提案されている距離減衰式では、一様なQ構造が仮定されているために異常震域を表現することができない。そのため、やや深発地震に関して、距離減衰式から予測される地震動強さは、太平洋側地域で過小評価、日本海側地域で過大評価となることが予想される。 B. 検討の方針やや深発地震における地震動強さの予測値を改善するために、特異なQ構造を考慮した距離減衰式を新たに開発することが望ましい。しかしながら、中村・植竹(2002)や関根・他(2002)など、最近推定された構造であっても、用いられているグリッド間隔が粗く、図2.4.2-1に点線で示されているLow-Qの領域の境界を決定することができないため、Qによる減衰をモデル化することが困難である。そこで、本検討では、K-NET及びKiK-netの強震動記録による最大振幅の観測値と、既存の距離減衰式による予測値との比較を行うことによって、距離減衰式に適用する補正係数を求めることとする。対象は、司・翠川(1999)による、断層最短距離を用いた距離減衰式(以下では、基準式と呼ぶ)とし、最大加速度及び最大速度の両者について、それぞれ補正係数を求める。 C. 補正係数の導出(1)使用するデータ 1997年1月1日から2002年6月30日の間に茨城県沖以北で発生した、太平洋プレートの沈み込みに伴う地震のうち、気象庁マグニチュードが5.0以上、震源の深さが30kmから153km、K-NETで10観測点以上の記録が得られている地震を対象とした。表2.4.2-1に地震に関する諸元を、図2.4.2-2に震源分布を示す。本検討では、K-NET及びKiK-netの東北地方と北海道地方の観測点で得られた強震動記録を用いる。最大加速度については地上の観測値を用い、最大速度については加速度記録にカットオフ周波数が0.2Hzのローカットフィルターを施した後に積分し、さらに、司・翠川(1999)と同様の手法によって評価された地盤増幅率をもとに、工学的基盤(S波速度600m/s)上での値に変換したものを用いる。本検討では、気象庁によって推定された震源位置における点震源を仮定して震源距離を求め、モーメントマグニチュードは気象庁マグニチュードと等しいとする。 (2)太平洋側と日本海側の振幅の違い 最大振幅の観測値と基準式による予測値の比較を行う。例として、図2.4.2-3に2002年12月2日の岩手県南部の地震による、最大振幅の観測値と基準式を示す。最大加速度、最大速度のいずれにおいても、震源距離が約300kmを境界として観測値の減衰の傾向が異なっている。そこで、まず、震源距離が300km以内の観測点記録について検討する。同一の震源距離に対して、観測値に大きなばらつきが見られるが、これは、主に異常震域による太平洋側と日本海側の振幅の違いによるものと考えられる。ここで、観測点から海溝軸までの最短距離Rtrを導入すると、Rtrが小さい太平洋側の地域ほど振幅が大きくなることが予想される。図2.4.2-4は、最大振幅の観測値と基準式による予測値の比obs/preとRtrの関係を示しているが、Rtrが小さくなるほど比が増加しており、観測値が大きくなっていることが分かる。いま、obs/preの分布を
の近似式で表すこととする。なお、ここでは、logはすべて常用対数を用いている。最小二乗法により、係数a1及びb1を各地震の最大加速度、最大速度のそれぞれについて求める。これらの係数a1、b1と震源パラメータとの関係を調べたところ、震源の深さHへの依存性が認められる(図2.4.2-5)。そこで、係数a1、b1をさらに
の近似式として表し、最小二乗法により、係数c1及びc2を最大加速度、最大速度のそれぞれについて求める。その結果、最終的に式(2.4.2-1)は、
と表される。ただし、式(2.4.2-3)は最大加速度、式(2.4.2-4)は最大速度についての関係をそれぞれ表している。なお、図2.4.2-5において、係数a1、b1がマグニチュードに依存しているようにも見えるが、これは、マグニチュードの大きな地震のほとんどが深い地震であることから、震源の深さの影響が現れているものと考えられる。 (3)遠地における減衰の傾向の変化 次に、震源距離が300kmよりも遠い観測点記録について検討する。ただし、ここでは、震源距離が300kmよりも遠い観測点記録が5点以上あり、かつ、震源距離が500km以上の観測点記録が2点以上ある13地震を対象としている(表2.4.2-1)。また、基準式の適用範囲は震源距離が300km以内であるが、ここでは外挿して用いている。遠地の観測点では、震源距離が遠くなるほど、観測値が基準式から離れていく傾向が見られる。ただし、同一の震源距離に対する観測値のばらつき幅は、近地と大きな差が見られないため、太平洋側と日本海側の振幅の違いは、遠地の観測点においても現れていると考えられる。その影響を除くため、ここでは最大振幅の観測値と、基準式に対して先に求められた補正係数1を適用して求められる予測値の比obs/pre1と震源距離Rの関係について調べる(図2.4.2-6)。震源距離が遠くなるほどobs/pre1が増加する傾向が明らかである。そこで、obs/pre1の分布を
の近似式として表し、最小二乗法により、係数a2及びb2を各地震の最大加速度、最大速度のそれぞれについて求める。これらの係数についても震源パラメータとの関係について調べたが、依存性は見られなかった(図2.4.2-7)。したがって、それぞれの係数について、平均値を用いることとする。その結果、式(2.4.2-5)は、
と表される。ただし、式(2.4.2-6)は最大加速度、式(2.4.2-7)は最大速度についての関係をそれぞれ表している。 (4)補正係数 以上で求められた観測値と基準式の間の関係から、最大加速度PGA、及び最大速度PGVの予測値を
のように、補正係数A1とA2、あるいはV1とV2を用いて求めることによって、精度の改善が期待できる。ここに、Apre、Vpreはそれぞれ、基準式により求められる最大加速度と最大速度であり、観測点から海溝軸までの距離Rtr、震源の深さH、及び震源距離Rの単位はkmである。以下ではA1とV1を補正係数1、A2とV2を補正係数2と呼ぶ。 D. 補正係数の適用とその効果 図2.4.2-8に、補正係数を適用して求められた地震動の最大振幅の予測値、及び基準式のみによる予測値の対数標準偏差(常用対数)を、解析を行った地震ごとについて比較したものを示す。基準式のみにおいて標準偏差が0.3よりも大きな地震は、補正係数の適用によってその値が0.3程度まで小さくなっている。補正係数の適用による標準偏差の改善は、震源が深く、規模の大きな地震で顕著である(図2.4.2-8b、c)。これは、震源が深くなるほど補正係数1の効果が、地震の規模が大きくなるほど補正係数2の効果が強く現れるようになるためである。 E. 今後の課題 今回の検討は、東北及び北海道地方のみを対象とした。これは、関東地方に関しては、太平洋プレートとフィリピン海プレートの両者が沈み込む複雑な構造の上にあり、図2.4.2-1のような二次元的な構造を仮定できないためであり、関東地方よりも西の地域に関しては、異常震域が現れるやや深発地震の数がほとんど発生しておらず、強震動記録が得られていないためである。したがって、今後、これらの地域について検討を行うことが必要であろう。 参考文献
|